Adventures in Wordle
I got to playing this fad word guessing game called “Wordle“. As seen below, one can guess 6 times and gets hints: green if the letter is an exact match with the goal, yellow if the letter is in the target at a different location (and there can be multiple letters in the case I guess two “d”s for “dodge”)., and black if the letter is not in the goal.

It turns out checking the webpage source results in an “official goal list” of size 2315 (whereas one can guess with a list of 12,972 5 letter words). I didn’t know this initially. It makes a pretty big difference. There are two possible official goals remaining after guessing “lovey” and “edits” above, whereas there are 13 from the full list. In either case, my “human” guesses were lucky.
As a human, my intuition was to play words that get the vowels first, such as “anime” and “yours”. Next, if nothing came to mind, I’d just check a reference website for help, such as https://www.bestwordlist.com/c/i/2/5letterwordswithispage2.htm. Maybe I’d use some intuition, aka common-word priors, to prune the words.
In this case, fuck, it didn’t work!

Apparently one may want to gather more information than cycling through greedy possibilities!
A friend ventured the question: could there be a trivial strategy of 5 words such that the answer is always determined in the 6th move? Being an advocate of almost brute force, I decided to just check the ways in which we can get 25 letters in 5 moves:

None of these combos work! Nor do I know some of these weird words: “vozhd” and “waqfs”?
Even over the official goal list, the best option is [‘bunje’, ‘curst’, ‘flimp’, ‘gawky’, ‘vozhd’], which contains 24 letters and misses 48 / 2315 words. Not too shabby.
Alas, I was lazy and filtered out some duplicate word combos if they covered the same letters (even though the word order does matter). So this is no proof that such a quintuple doesn’t exist.

What’s next is to look for a deterministic strategy that solves the game. This means there will be one fixed starting word. I chose ‘salet’ via a process to be outlined below:


Next, the strategy needs to choose one word to play given it receives this hint (‘Green Black Yellow Black Black’). There are 73 possible words and the guess ‘olios’ will reduce the number of possibilities to 9 (and over official goals, there are 24 possibilities; ‘plouk’ reduces the number to 3).

Now the following words remain: [‘swill‘, ‘skirl’, ‘skill‘, ‘shily’, ‘swirl‘, ‘spill‘, ‘shill’] (official in bold). Curious that ‘shill’ is not in the list 😋. It was apparently just curated by the developer’s girlfriend. “Perky” will let us know which official word is the goal, but let’s play ‘chalk’, which reduces the full list of words to 2:

Now we’re down to two possibilities, [‘swill’ and ‘spill’], in both lists of goals. So we can just guess. Voila, the simple strategy works 😏.
Does it work on every single word?
- Official 2315 words: yes!
- A solution is easily found that solves the words in the following number of steps:
- [‘2 : 45’, ‘3 : 283’, ‘4 : 1557’, ‘5 : 430’] — average score: 4.02 guesses / goal
- Hard examples: spout, icily, honey, money, giddy, puppy
- Easy examples: solar, tease, salty, saint
- Official 2315 words in hard mode (where all yellow and green hints must be used in following guesses): yes!
- Curiously, this solution is also easily found!
- [‘2 : 90’, ‘3 : 835’, ‘4 : 1143’, ‘5 : 224’, ‘6 : 23’] — average score: 3.67 guesses / goal
- Hard examples: craze, graze, poker, power, witty, willy
- Easy examples: heart, tease, tacit, cello
- Full 12,972 word list: nope . . ..
- The best I’ve found is:
- [‘1 : 1’, ‘2 : 20’, ‘3 : 763’, ‘4 : 6451’, ‘5 : 5113’, ‘6 : 614’, ‘7 : 7’, ‘8 : 3’] — average score: 4.43 guesses / goal
- The 7 guess words: tests, vests, zests, fills, jills, lulls, fulls
- The 8 guess words: zills, gills, lills
The YouTuber 3Blue1Brown, who does amazingly dazzling math education videos with illustrative graphics, posted a video on ‘solving’ Wordle. He sees this as an opportunity to introduce information theory concepts such as the entropy: how much uncertainty is there the set of official words? 1 bit means that there are two options so letting you know “one piece of information” will tell you which is which. To choose a move, 3b1b (Grant Sanderson) asks what the expected entropy will be over all possible goals and chooses the move that has the greatest expected decrease. This is spiritually very similar to my choosing the word with the best worst-case hint bucket (that is, the words with the same hint). I framed this as a greedy mini-max problem. It’s greedy because I’m only doing what’s best “for the next move”, which might not be best overall.
The way that I got “salet” was to calculate the largest hint bucket for each word. For example, there are 865 words for which the hint to “salet” as a guess is “BBBBB” such as “humph”, “pound”, and “corny”. For “crane”, on the other hand, there are 1578 with the all-black hint. “Serai” actually has the worst-case hint bucket of “BBBYB” containing only 697 words! Next, I took the top one thousand words and saw what the best combination of two words here is. I think it was so slow I gave up part-way through. “Salet” and “irons” in two moves had a worst-case bucket of 129 words and I realized “irony” is better, bringing it down to 127. 3b1b wrote more efficient code and apparently checked all two-move combinations, resulting in “crane” and “salet” being the best starters, too 😉.
There’s also the discussion as to what the best goal is. Do I just want to solve every word in under 6 guesses? 6 is pretty arbitrary. As an example, on the full list of words, I have a ‘solution’ with 43 goals that took 7 guesses but on average wins in 4.32 guesses instead of 4.43. So on average I’ll do better but lose a bit more. There’s the decision problem: is there a strategy to always solve Wordle within k moves? What is it? And there’s the optimization problem: if there is a solution, what is the best possible solution by criteria m?
I downloaded and ran 3b1b’s code. It was pretty spiffy (tho not as fast as I’d have expected). It had two-step lookahead parameters and some brute force optimization. Increasing these a bit, it was appearing non-trivial to improve upon my solutions. One really cool thing 3b1b did is to calculate the word frequencies under the assumption that “more common words are more likely to be the goal” because, while we know there is an “official word list”, this could be changed at any time, so why design solutions that only work for it? The full list is less likely to change 😉. I tried a lot of incremental hacks to improve the solution to no avail. Most of the blog posts I’ve seen claiming to have “solved wordle” seem to focus primarily on the official word list.
My friend suggested a basic proof that solving hard mode is impossible (and his ASP solver indicates this for some words):
- Consider the following list of *ILLS words: [‘bills’, ‘cills’, ‘dills’, ‘fills’, ‘gills’, ‘hills’, ‘jills’, ‘kills’, ‘lills’, ‘mills’, ‘nills’, ‘pills’, ‘rills’, ‘sills’, ’tills’, ‘vills’, ‘wills’, ‘yills’, ‘zills’]
- Once ‘i’, ‘l’, or ‘s’ is hit, it must be used in the next guesses, which can result in needing to guess one different letter each move, thus failing to make it in 6 steps.
- Let’s consider an example attempt:
- >
hs = sorted([(score_hint_distribution(word, hills), word) for word in words]; hs[0]- (14, ‘chynd’)
- The word ‘chynd’ reduces the number of possible words to 14, making it a good candidate to solve *ILLS.
- >
m1 = get_hint_distribution_with_words('chynd', hills); m1{'bbbbb': ['bills', 'fills', 'gills', 'jills', 'kills', 'lills', 'mills', 'pills', 'rills', 'sills', 'tills', 'vills', 'wills', 'zills'], 'gbbbb': ['cills'], 'bbbby': ['dills'], 'bybbb': ['hills'], 'bbbyb': ['nills'], 'bbybb': ['yills']
- Now there are 4842 words we can play (*possibly underestimated). Of these, ‘bortz’ reduces the possibilities to 10 without matching ILLS and then ‘swamp’ takes us to 6.
- Continuing this process manually, I got a 7 move solution: chynd, bortz, swamp, flegs, lusks, vills, and jills.
- But I wrote a brute-force solver that orders the moves by worst-case hint-bucket size and just keeps trying them all in order. And it solves this in hard mode in multiple ways:
- Chynd, bingy, jimpy, vifda, lisks, kills — for one 6 word win.
- Crwth, bingy, jimpy, vifda, lisks, sills — for another 6 word win.
- The search space involves some nifty words (that I really don’t know), so it’s hard to determine that there is no solution.
- Compiling a list of challenging word sets (*ECKS, *ESTS, *ARKS, etc), I think it won’t take that many of them to break hard mode. But I did my initial experiments on hard mode with the assumption that black hints could not be re-used either, which speeds up computations a lot. In that scenario, I only needed one more hard word set to kill all starter words in hard mode. Then I got lazy when I realized I misunderstood the hard mode game settings 😂😂😂.
Curiously, it also turns out that *ILLS breaks the starting word ‘salet’. Weird, right? It’s one of the best starting words if you want to win quickly on average but you can’t even solve all 19 *ILLS within 6 moves. Only ‘s’, ‘l’, and ‘t’ match the letters from *ILLS but ‘s’ and ‘l’ are in every word in the set, so they don’t provide discriminatory information here. One would need to guess a word with three ‘l’s or two ‘s’s for that. So there are still 18 letters that need to be disambiguated, now in 4 moves, which is 4.5 letters per move and is asking too much. I think this is a bad enough situation that I might be able to actually “just prove it.”
So I decided to see if I could find a minimalish set of words that breaks each stater word. This is a bit like looking for an unsatisfiable core. I’d start with *ILLS and keep adding other hard word sets in until the word is broken. This turned out to be rather frustrating, which I think is due to the nature of the computational complexity of the problem.
Interlude on Computational Complexity
The computational complexity of a problem is how many resources it takes to compute solutions to the problem. For example, if you want to know whether a word can be played in Wordle, you may naively need to check all 12,972 words to see if it’s in the list or not. This is called \(O(n)\) where \(n\) is the number of elements in the problem (the number of words in this case). However, this depends on how the word list is structured. If the word is longer or shorter than 5 letters, then it’s very easy to know that it’s not in the list. This is constant time (\(O(1)\)), as it only depends on the length of the word, which is relatively short. If I bucket every word according to the first letter, then to find out if ‘super’ is valid, I only need to check the 1565 words starting with ‘s’. And it gets even better: maybe we bucket words by letter all the way down, so next, we want to look at all words starting with ‘su’, which gets us to only 76 possibilities. By the time we get to ‘sup’, there are only 3 words: ‘super’, ‘supes’, and ‘supra’. This way of structuring data is called a Tree. In general, this method should let us look up words in time \(O(k \cdot l)\), where \(k\) is the length of the words and \(l\) is the number of letters, which is much smaller than \(n\).
Dealing with data that has a total ordering is really handy. That is, when you know that, say, \(1 < 3\) (one is less than 3) or ‘a’ < ‘b’ < ‘z’. If I want to sort the list of moves in Wordle, then I can use a Radix sort (also called a bucket sort) which is to do as above: throw all words beginning with ‘a’ into one bucket, ‘b’ into another bucket, and so on. Then in the ‘a’ bucket, I create a new bucket for each letter, so words starting with ‘aa’, ‘ab’, and so on each get their own bucket. After 5 steps (or fewer), I’ll have a handy tree with the data lexicographically sorted: ‘aahed’, ‘aalii’, ‘aargh’, ‘aarti’, ‘abaca’, . . . 😉. A practical caveat is that this method depends on the size of the words: if the data elements are hundreds or billions of digits long, then it’s highly inefficient!
If we sort the list of words instead of building a tree, then there are ways to search for a word in \(O(\log(n))\) time. The binary search algorithm, also called logarithmic search, is to look at the middle element, ‘louse’, and then because ‘super’ is later in the alphabet, to look for the middle of the second half of the list, which is ‘sechs’. As you can see, we will narrow in on ‘super’ pretty quickly. In this case, \(\log(12972) \approx 9.47\) is quite a bit bigger, so working with a tree is probably more efficient, but it’s a lot faster than finding a word without structuring them first. So if one is doing many lookups, it’s worth spending some time to order the data.
How long does it take to sort a list? In general, computer scientists like to imagine the scenario where we can compare any two elements to determine whether \(x < y\), \(x = y\), or \(y < x\) but we don’t know that, say, ‘abaca’ will likely be near the start of the list by virtue of the alphabetic order. The simplest idea in my mind is called Insertion sort: we just go through the list and sort it from left to right. If an element is not the biggest we’ve seen so far, we find the right place for it. On average, we’ll need to make \(O(n^2)\) comparisons, where \(n\) is the length of the list. This is on the same order of magnitude as just comparing each element with every other element! 😱
Quicksort is a really cool and simple approach that on average does way better (but performs the same in the worst case). Start by picking a random element in the list and partitioning the rest of the elements depending on whether they are Greater or Lesser than this ‘pivot’ element. Then ‘sort’ each partition in the same way by picking new ‘pivots’. This is a “divide-and-conquer” algorithm. On average, you’ll sort the list in \(O(n\log(n))\) steps but you could get unlucky. (Mergesort is a similar approach that does this well no matter what but I think it can be slower on average in practice. If you haven’t done it before, I suggest playing around with some sorting algorithm animations.)
Sorting and word lookup are much easier problems than Wordle, however. They belong to the complexity class called “polynomial time“. P is the class of all problems with a computational complexity of \(O(n^k)\) for some (natural) number \(k\). We tend to think of P as consisting of low-complexity, ‘easy’ problems. The class also has good properties such as being able to write a polynomial-time algorithm that calls other polynomial-time algorithms, knowing it’ll still be in P. In practice, \(O(n^{10,000})\) would be pretty bad and the big-O notation can hide constant factors, such as perhaps “\(1,000,000,000,000 * O(n^{10,000})\)”.
Intuitively, the next complexity class would be “exponential time” (EXPTIME), when the algorithm takes \(O(2^n)\) steps even in the best case. Generalized games can provide an example:
Generalized Go or Chess where the board can be as large as needed are EXPTIME hard. In the worst case, to determine if black or white will win, you just have to explore every single branch of the game tree. It’s important to have gameplay that allows the number of moves to become exponential in the size of the board, such as the Japanese Ko rules. In Chess, you will want to remove the rule that says it’ll be a draw if you go 50 moves without capturing a piece. One could also think about looking for the “perfect” game of Chess (but it’s possible there’s a really nifty trick that allows Chess to be solved more effectively).
Another classic example is “determining whether a program halts in \(k\) steps”, which due to the ‘undecidable’ nature of the halting problem, means you just need to simulate every possible run of the program. Both of these are actually EXPTIME-complete, meaning that any other exponentially hard problem can be translated into a generalized Go game! Does this lend some truth to the idea that most situations can be understood by analogy to Go games . . . 🤔 😏?
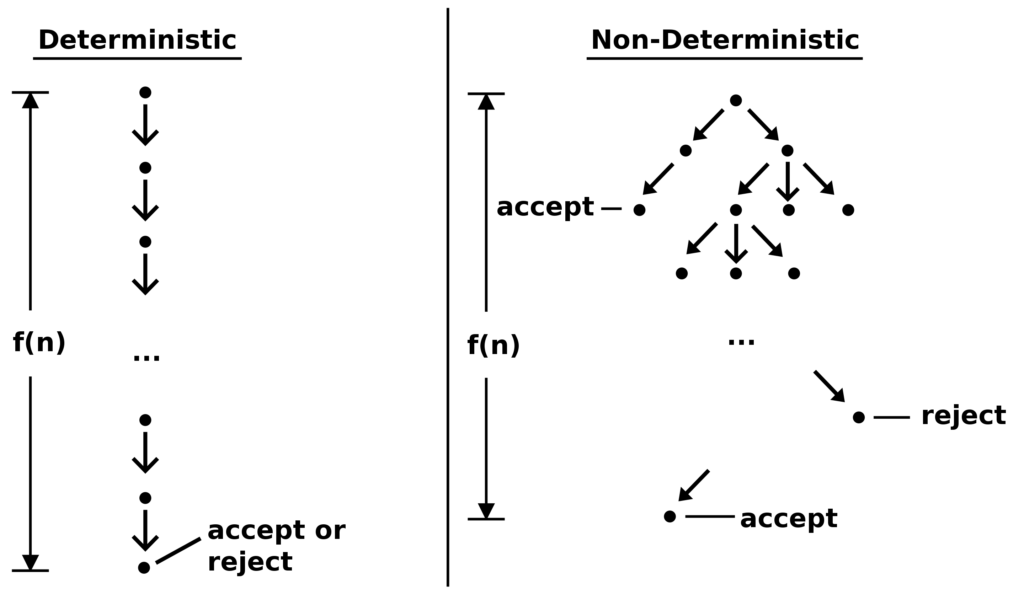
The complexity class relevant to Wordle is a bit more subtle. It’s called “Non-Deterministic Polynomial Time” or NP. This relies on the idea of non-deterministic computation. I like Wikipedia’s image:
I’m used to thinking of deterministic computation as a sequence of operations. First I set “x = 1”, then if “x > 0”, I do something, and otherwise I do something else. Suppose I want to explore ten possible starter words to solve Wordle, then I have to just pick an order to try them in. But what if you could parallelize and just do all ten at once? Or, for the purpose of theoretical analysis, assume that it’s not determined which word I start with and each time I need to make a choice, I magically get the luckiest possible choice. This is like assuming I’ll always guess the answer in move one when playing Wordle. So, theoretically, there’s always an answer in one move!
Isn’t this silly? — A little bit, yeah. Non-deterministic computation is a way to talk about the existence of “short” solutions.
There’s another way to think about the complexity class NP in terms of “verifying solutions”. Consider the Subset Sum Problem where one is given some numbers, \(\{1,2,3,4\}\) and wants to know if a subset of these numbers sums to \(7\). Naively, you would need to check the sum of every possible subset (\(\{1\}\), \(\{1,2\}\), \(\{2\}\), \(\{1,2,3\}\), etc), which involves \(4 * 2^4\) (\(n * 2^n\)) steps. But if I tell you that the answer is \(\{1,2,4\}\), then you can easily check this in Polynomial time (or linear time, lol). This is what the “non-deterministic” computation says: if there is a P-time solution and you could search every path at once, then you’ll find a solution in P-time. And this is why it’s important that in Generalized Go, the game can become exponentially long in the board size: even if you could play all possible Generalized Go games at once, it might still take exponentially long. Yikes 🤯😋.
One of the most infamous questions in computer science is whether P = NP [W]. Given that all NP problems have P-time solutions, maybe there is some really sneaky, clever way to find them instead of resorting to brute-force search! Most computer scientists believe that they are not equal, however, and that one must sometimes get lucky or do a brute-force search over all possibilities.
My friend mapped the NP-complete Dominating Set problem onto Wordle. A dominating set is a set of vertices, \(D\), in a graph such that every vertex is either in \(D\) or adjacent to a vertex in D. The idea is that when solving Wordle, I want to find a set of up to 5 words that rules out every word except for the goal, which is a bit like covering a graph of the words. In his example, a graph with 6 vertices needs words made up of an alphabet with 43 letters to be solved via playing Wordle. And if every NP-hard problem can be translated into a Dominating Set Cover problem and that can be translated into a Wordle problem (with very long words), then wordle is also NP-complete. It’s pretty nifty.
Let’s look at what this actually means for Wordle. There are \(n = 12,972\) words that can be played. In a single game, there’s one goal such as ‘peach’. We can always get lucky (as the non-deterministic computer would, trying every possible move in parallel). But it’s more interesting and realistic to ask if we can play a series of moves whose hints rule out all \(12,971\) words other than ‘peach’ so that we are guaranteed to win within 6 moves. If we take a really naive approach, there are 12971 words to choose from in moves 1 to 5. So we would check every single combination of the words to see if one works. Maybe we don’t need 5 moves, so we can try single words, then pairs, triples, quadruples, and then quintuples. How many of these are there?
- \(12972^1 = 12,972\)
- \(12972^2 = 168,272,784\)
- \(12972^3 = 2,182,834,554,048\)
- \(12972^4 = 28,315,729,835,110,656\)
- \(12972^5 = 367,311,647,421,055,429,632\)
367 quintillion is a lot of possibilities to try (and this is just for one goal 😂). As we saw earlier, if we play ‘salet’ and get the hint ‘BYBYB’, there are only 301 possible goals that would give this hint. If we next play ‘dearn’, there are only 18. And then after playing ‘humpy’, ‘peach’ is the only possible goal. So it’s possible to pinpoint ‘peach’ within 3 moves. And when I tell you that the guesses [‘salet’, ‘dearn’, ‘humpy’] solve ‘peach’, it’s not hard to verify this (in P-time).
As expected of an NP-complete domain: naive approaches blow up in your face even when simple solutions work 😏. One can often find smart tricks to solve ‘many instances’ of NP problems quickly. As an example, using the official word list of 2,315 goals with 12,972 guesses, the search space still blows up, but the greedy strategy always works. Whereas, with all the words as goals, a deterministic strategy starting with ‘salet’ will always lose. And the greedy approaches 3b1b and I tried don’t work for any starting word.
As an emotional and technical note, trying to make sense of the related computational complexity here rather confused me. It seems the NP-complete nature of the problem is finding the smallest solution: this in principle involves checking every possible combination of words, which will blow up to something like \(O(2^{|words|})\) (– the general number of possible subsets –). The first nitpick is that it’s really easy to check that the smallest solution is at most 8 words long. The greedy strategy does this. The second nit-pick is that if we want a solution of a specific size \(k\), then the problem is “only polynomial”: \(O(|words|^k)\). This is still really fucking big as we saw before and brute-forcing would take ages on a personal computer. And our goal is with \(k = 5\), so the problem we’re solving is kinda just P-time. It turns out this is the same for the Dominating Set problem. The core problem remains, however: most words probably provide unique information that could contribute to a hard-to-find solution.
Another nuance is that I don’t just want a solution for each goal separately. Consider the following example:
- Goal: ‘vests’.
- Solution: ‘tares’, ‘varas’, ‘tassa’
- Goal: ‘nests’.
- Solution: ‘tares’, ‘narre’, ‘easts’, ‘rasta’
Maybe I found out that there is a solution for every goal but when I actually play Wordle, I only see one hint at a time and then have to choose what to play next. In the above cases, after playing ‘tares’, the hints are the same: YBBYG. In this situation, I need to find one word to play that works for both ‘vests’ and ‘nests. So I want to find solutions for all 12,972 goals that can be glued together (in such a manner that whenever the hints for two words are the same, the next move is the same). A solution is a tree with a starter word and then one move for each possible hint. The leaves of the tree should be hint-buckets with only one possible goal remaining. If the tree has a depth of 6 or smaller, then we will always win. This is what I reported above for the official word list (and the full word list with a depth of 8).
This doesn’t actually change the complexity class of the problem. Calculating the hint-buckets is \(O(n)\) and doing this for every word is \(O(n^2)\). Going through all possible solution trees (in order based on how well the words split the remaining possible goals) is still just playing in this “\(|words|^5\)” space. So it’s practically speaking a messy P. This is actually one of my pet peeves with computational complexity: the big-O notation often hides many details pertaining to the nature of the actual problems one is working with. But if one wants to be able to solve “every problem”, then worst cases can become relevant, as seen in how ‘salet’ is a good move that nonetheless fails on a few goals. Another way to make generalized Wordle more difficult is to want solutions with words that don’t have overlapping letters (which resembles an independent set of a graph). I think such a solution may not exist but try and find out if you’re curious 😉😏.
[If you’d like to read up on Computational Complexity, this website looks retro and cute: https://complexityzoo.net/Petting_Zoo. I also absolutely recommend Quantum Computing Since Democritus by Scott Aaronson [gr].]
Back to trying to solve Wordle, after realizing that our “best starter” word, ‘salet’, can’t possibly work as a full solution (because it already fails on *ILLS), I started wondering if perhaps there doesn’t exist ANY solution for \(k = 6\). Unfortunately, it can be hard to show that a solution is not possible. I really want to avoid searching through all \(12972^5\) possibilities. In the case of *ILLS, it’s possible to do some reasoning to rule out many possible word combinations but it’s less clear how to proceed like this in general.
I decided to try gathering a hard set of words by finding words that solve *ILLS (such as ‘zymic’) and seeing where they fail on the full word set:
- *ECKS, *ESTS, *UMPS, *EALS, *OOKS, *OCKS, *ELLS, *ARKS, *ERKS, *ENTS, *ERRY, *OLLY, *IGHT, *AILS, A**FS, A**ES, A**ED, AAS, O**ED, O**ES, A**AR, I**ES, and I**ER
I turned the greedy solver into one that does a brute-force search: if the ‘best guess’ doesn’t work, it keeps trying them in order. To speed this up, I decided to create a ‘learning’ system by storing in a Python dictionary each set of words that can’t be solved via a good 5th move. This way the brute-force search near the bottom of the trees can get faster as I go. (I also tried adding words that can’t be solved via a good 4th move etc.)
This was working pretty well to gather some unsolvable words: ‘salet’, ‘fuffy’, ‘reais’, ‘tears’, ‘reaps’, horns’, ‘hosts’, ‘reals’, ‘reaksy’, ‘yuppy’, . . ..
However, I noticed that ‘crane’ (one of 3b1b’s best words) solved *ILLS after scrolling through many other guesses and arriving on ‘swift’. ‘Crane’ kept crushing my challenging word sets, relying on ‘swift’. I got curious and decided to see how ‘swift’ would do. ‘Swift’ really quickly (relying on some of the learning) went through almost all of the challenging words. But maybe there is some tricky word combination that foils it. I eventually switched gears and decided to try to solve Wordle again after all.
I decided to try doing it pseudo-manually: get a greedy solution with ‘swift’ in 7 moves instead of 6 and then find the branches of the solution tree where it fails. Maybe I can do a brute-force search near the bottom more easily. This helped but the hint ‘YBBBB’ was broken from the top and the bucket contained 2133 words. The ones of the form [“based”, “babes”, “laves”] were especially challenging (and I almost thought it’d fail after all!). I tried to add yet another level of learning via storing failed word sets in a dictionary (and also remembering cases where I have a solution) but it seems that either I introduced a bug somewhere or I corrupted the memory.
Approaching the point of giving up, I decided to reset the memory and jumpstart the solver to always try ‘lover’ as the second move. “Swift lover” seems cutesy 🤭. To my surprise, this actually worked and I got a solution =D. 🥳🥳🥳
At first, I thought it was because I reset the memory but “swift”, “crane” and just going with the greedy recommendations ran for a day or so without solving it. The conclusion is that I got lucky. I’m not sure why ‘lover’ is such a good second word here. Is it the combination of common letters, vowels, and the rare distinguisher ‘v’? 3b1b spent some time discussing how ‘w’ is really useful when you get a match but as a rare letter, it otherwise doesn’t help much. However, handling the hard cases seems more important for finding a solution, so Bob’s your uncle and Fanny’s your aunt. The solution is:
- [‘1:1’, ‘2:26’, ‘3:834’, ‘4:4931’, ‘5:5812’, ‘6:1368’]
- Average score: 4.59
This performs worse on average than the greedy solution’s score of 4.43.
Does there exist a full solution in 6 moves that performs better? That seems not unlikely, but finding it may prove tricky. And as to hard mode, 🥱, I’m ready to move on. This took longer than expected 🤓😛
[I’ll upload some partially cleaned code and the solutions on GitHub shortly.]
Lessons Learned
I found getting into a relatively easy problem that can just be solved rather fun!
My current field of Automated Theorem Proving is a bit more difficult.
Propositional logic can be solved by checking all possible variable assignments, so it’s NP-complete if you want to satisfy a formula and co-NP-complete if you want to show that a formula is a tautology. For example, \(P \wedge Q\), can be satisfied by setting both P and Q to be true and this can easily be checked, but there’s no short way to show that a formula can’t be satisfied in general. A tautology is a formula that is true for all possible variable assignments. The formula \(P \wedge Q\) is not a tautology because it’s false if P and Q are both false and this can be quickly checked. Co-NP is the class of problems where “no” instances can be easily verified. The following formula is an example of a tautology: \( (A \wedge (A \to B)) \to B \), if A is true and A implies B, then B is true. It works because material conditionals (\(\to\)) are considered to be ‘true’ if the antecedent is ‘false’.
My work is on proving conjectures in First-Order Logic, however. Now we talk about “decidability”, whether a problem can be solved at all, ever, or not rather than how long it’ll take to find a solution in the worst case. First-order theorem proving is “semi-decidable“, which means that if a conjecture is a true theorem, then a proof can eventually be found (if a complete search procedure is used); however, if the conjecture is not true, then the theorem prover may never terminate its search.
This is similar to the case for computer programs in general. Famously, one cannot, in general, determine whether a program halts or not but, speaking tautologically, if a program will halt, you could eventually find this out by “just running it” for as long as it takes, so it’s semi-decidable, too. There’s a generalization of this called Rice’s Theorem that any “non-trivial semantic property” of a program cannot be decided. One example would be determining whether a program adds two numbers, such as:
def plus(a,b):
return a + bBy non-trivial, one means that the property isn’t true of all programs (or of none). This is also called vacuous truth. And by semantic, one means that the property is one of a program’s behavior, not of its syntax. So we’d test “plus” by what it does when we input two numbers and not by saying, “does it contain ‘a+b’ or some syntactic variant thereof?”
The proof by contradiction of Rice’s Theorem is so beautifully simple, I’ll include a sketch of it here. So assume we have a perfect “is_plus_function” program that can tell us whether any program is a plus function or not:
is_plus_function(plus)
>>> TrueNow this function is so magical that we can easily solve the halting problem:
def halts(function, input):
def magic(a, b):
function(input)
return a + b
return is_plus_function(magic)If the “function” halts on the given “input”, then by “magic” returning “\(a + b\)”, our “is_plus_function” will tell us that this is a plus function (– oh, and by the way, that means the “function” halts –). And if “function” doesn’t halt? Well, then “magic” also runs forever and never gets around to doing the addition, so behaviorally speaking, “magic” is not a plus function. Voila, we’ve solved the Halting Problem. Which can’t be done, so by contradiction, we know that there can be no “is_plus_function”. QED 🥲.
Also, note that a shallow analysis of the syntax might mistakenly think that “magic” is a plus function because it looks almost the same as “plus”. “Function” probably doesn’t change the values of “a” and “b”, so one would naively assume that it is indeed a plus function.
And this is the domain of my automated theorem proving work. Solving all possible interesting conjectures is not known to be possible and even though I generally work with known theorems from Mizar (or Isabelle), if we miss an axiom by mistake (as automatically choosing axioms is part of the task), it could be unprovable and run forever. Thus the focus is generally on improving learning techniques than on actually solving open problems. [As an aside, a long-standing open conjecture that was hammered on for years with Prover9, an automated theorem prover, was solved recently and announced at AITP21. The AIM conjecture. Which is really cool 🤩🥳.]
To my chagrin, however, even a solvable problem with only 12,972 elements is not necessarily trivially easy. As a meta-lesson, I find it really interesting how small changes to the problem set-up can make a huge difference in how easy it is. For example, solving for 2,315 goals was really, really easy (even in ‘hard mode’) yet the full set took ages. Removing 10 words from the set would probably make it much easier. Adding 10 artificial adversary words might make solving Wordle in 6 moves impossible?
Moreover, what’s the goal anyway? Who sets it? Most people I saw talk about “solving Wordle” online seemed to mainly concern themselves with the official goal list (and I may have, too, if I hadn’t mistakenly assumed the full word list was the goal in the start 🙃). Some solved all but 14 (99.4%) with a word-frequency method and were satisfied. Donald Knuth assembled a list of roughly 5,000 five-letter words a while back with some differences from this one — should I try to gather all five-letter words in the English language as the goal [1][2]? And what about the size of the solution? If I want to find the smallest solution possible or the one with the lowest average score, then I’ll need to come much closer to searching every possible combination 🤯. Is finding a solution within 6 moves the hardest choice for this problem instance? I think (but haven’t proven) that 5 is not possible and 7 is pretty easy. I can exhibit a bit of a stubborn completionist streak but why does this exact problem setting matter?
I think this is a very important lesson when thinking about goals in life in general. I’m a big proponent of satisficing: aiming to sufficiently satisfy a desired threshold instead of aiming to do something perfectly or “as well as possible”. My adventures in Wordle really bring this lesson home: meeting a satsifaction criteria of 10 / 12,972 (99.92%) would be pretty easy. The last 0.08% took almost all of the effort.
The law of diminishing returns can turn up in many domains. Eating food is one example: at first the meal is utterly amazing and nourishes you. At some point you become satiated and can still enjoy eating (even though your body may not need the content). Eventually it becomes hard to stuff oneself with more and doing so can lead to painful and undesired consequences. The largest gains come from the first part of the meal 😊🤤. When learning language, the added benefit to learning 10 new words also decreases over time (but does it ever truly become negative? 😋).
Where might we be striving for perfection where, from a big picture view, perfection simply doen’t add much additional value? Ahaha, in machine learning, there’s even the idea of overfitting: adapting perfectly to one situation might make it very hard to adapt to changes. One also wants to optimize what one optimizes for: the current situation or the ability to generalize and transfer one’s skills to new domains!
I could rant for a long time about the desirability of highly competitive environments encouraging over-optimization. What do we actually want personally and as societies? If 5 competitors pour in 50x the resources trying to be the best when a much lower bar would satisfice us, is this a wise choice? Perhaps we could satisfice and direct this energy elsewhere, truly economizing (in the sense of organizing ourselves more energy efficiently).
Speaking of transfering skills among domains, given that all NP-complete problems can be mapped into each other, techniques that help with solving one should probably help with the others, right? The precise form of the problem does matter, so it seems possible that some problems may be more easily solved as SAT problems (like satisfying a bunch of formulas in propositional logic) and others as Dominating Set problems and if you can identify which is which, performing the translation might be worth it. Actually, SatZilla is a SAT solver that works by choosing which other SAT solvers to use based on profiling the specific problem =D.
When I was looking to show that Wordle is unsolvable, I realized I’d need to do something to speed up the brute-force search. Learning sets of words that can’t be solved in two more moves was a small start that led to a big speedup already. But then I noticed into a pretty big inefficiency right away. Have a look at the following two such word sets:
- (‘fills’, ‘jills’, ‘lills’, ‘vills’)
- (‘bills’, ‘cills’, ‘dills’, ‘fills‘, ‘jills‘, ‘kills’, ‘lills‘, ‘mills’, ‘vills‘, ‘wills’, ‘zills’)
The first is a subset of the second. This means that if I need at least 3 moves (when I only have 2) to solve (1), I will also need at least 3 moves to solve (2). Therefore I shouldn’t need to store (2) in my Python dictionary at all. The theorem prover I work with, E, has this feature using featuer vector indexing to check for “clause subsumption” (and also set subsumption) [E]. In this case we would say that (1) subsumes (2).
I really wanted a smart way to keep track of precisely which letters in which positions were the most difficult to solve in unison. Clearly 19/26 in the first position are challenging already but that’s not enough. I recalled that for SAT problems there’s something called Conflict-Driven Clause Learning, which is a method of identifying clauses that lead to conflicts and adding them to the problem to incrementally learn. Possibly with a decent encoding of Wordle as a boolean SATisfaction problem, this sort of approach could help narrow in on solutions (or on the letter combinations that confound us).
Re-inventing the wheel for the specific problem of Wordle might not transfer to new domains much, whereas SAT solving and (first-order) theorem proving are very general. Thus, if there is a next time, maybe I’ll consider just translating Wordle into another domain early on. If I still need some Wordle-specific hack, at least it will be done in the translation or in a more easily general domain. Aesthetically, I think it’d be a lot cooler to transslate Wordle into a graph, however 😎. I tried a lot of expedient hacks that seemed like they should probably be good enough. Ironically, given I like satisficing, it seems if aiming for perfection, it could be faster to just do things systematically or more properly from the start.

I also received some coding refreshers: it’s really easy to get 100x speedups here and there even in Python by doing things ‘a little bit smarter’. Working with E, a lot of the really tricky optimizations have already been done (hail Stephan Schulz), so it’s been fun fiddling around from the ground up. I don’t think much about Object Oriented Programming, so it was fun realizing a Wordle Assistant should be an object that keeps track of the move history. I also saw the value in simply trying half a dozen different ways of implementing basic functions: this sort of play must be why free and open source (FOSS) hobby coders have such 1337 skills.
The actual code is a mess and tells the tale of my thought processes, which I really love to honor. I also believe in allowing ourselves to show imperfections, so the uploaded code will include a lot more than a cleaned up, enterprise edition (but with a lot of deprecated clutter removed). The worst part is that the memory features are probably buggy and I’m ready to move on 🤷♂️😋. Anyway, you can see it on GitHub, with some examples of the Wordle assistent in action at Sketches of Playing with Wordle.
All in all, it’s been fairly fun.