A Graph Neural Network Over Mathematical Formulas

Note: the research this post discusses was not done by me. The hero is Miroslav Olšák and supporting researchers. He has a cute YouTube channel with an animated guide to the Essence of Set Theory. Thus, please forgive any errors in representation as they may not be due to the authors of the work. A slideshow by Mirek on the graph neural network (GNN) can be found here.

The achievement is sufficiently cool and seminal that I think it’s worth being written about. Moreover, I’m fucking glad someone got it kinda working (especially given my failed adventure into the graph neural network territory). This post is based on two papers:

1. Property Invariant Embedding for Automated Reasoning.
2. ENIGMA Anonymous: Symbol-Independent Inference Guiding Machine.

It may come as no surprise that this graph neural network (GNN) is also featured in my latest research papers.

Recall that we are still using extensions of the following procedure to featurize formulas:

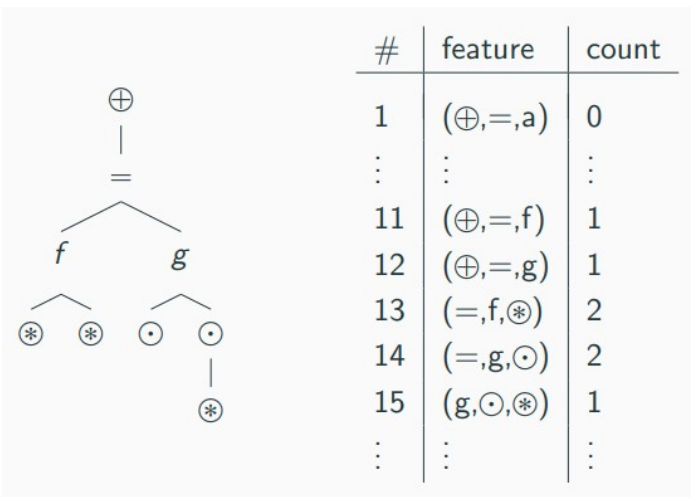
Term-walks of length 3 over the formula-tree are hashed into some hash-base and counted to produce a vectorial representation of the formula. This captures some of the ‘structure’ of the formula, which is the part we find meaningful. In ENIGMA Anonymous, Jan Jakubův et al replace the symbol names (e.g., ‘f’, ‘g’, or ‘are_equipotent’) with whether they are functions or predicates and their arities, that is, the number of arguments they take. In this case, the function symbols ‘f’ and ‘g’ are both of arity 2 and one of the Skolem symbols is of arity 1. The distinction between variables and Skolem symbols will allow the featurization to represent ‘f’ and ‘g’ differently, fortunately. The symbol-anonymized ENIGMA with gradient-boosted decision trees seems to work at least as well as the one with symbol names (and better in domains where, unlike in Mizar, names are not used consistently). XGBoost and LightGBM are generally used.

The dream is to give the AI the actual structure of the formulas, clauses, and their interrelations so that the mathematical data can be worked with as is (rather than via some hacky approximation). And at least if some feature vector is going to be used, can’t we learn this from the formulas directly?

There have been some attempts before such as FormulaNet, pictured below, which is still dependent on function and predicate symbol names. The image is also more evocative and better than those in our teams’ papers 😅. Mirek brings us even closer to the dream.

Clausal Interlude

The graph neural network is designed to accept a set of clauses, so let’s refresh what this means.

Logically, a set of clauses is implicitly stood to be connected via a series of ‘ands’ (\(\wedge\)), that is, all the clauses should hold true (for some interpretation). We work with conjunctive normal form (CNF) where each clause is represented as a series of literals connected by ‘ors’ (\(\vee\)).

In the examples, I used in the ProofWatch post, such as “\(Aunt(zade)\)”, ‘aunt’ would be a predicate symbol because the intended interpretation is to be ‘true’ if the constant symbol ‘zade’ represents an aunt. The clause specifying that aunts are female, “\(Female(X) \vee \neg Aunt(X)\)”, also includes a variable symbol, “\(X\)”. The following are both literals: “\(Female(X)\)” and “\(\neg Aunt(X)\)”.

Terms are considered mathematical objects that predicates apply to. I’m using the convention that predicate symbols are upper-case and function symbols are lowercase. What if I want to have a formula that says, “If someone is human, then this someone’s mother is female”?

• \(Human(X) \to Female(mother(X))\)
• \(\neg Human(X) \vee Female(mother(X))\)

“\(mother(X)\)” is a slightly more complex term with a function symbol. Technically “\(X\)” is a subterm as variables are terms. We could also have fun: “\(mother(mother(X))\)”. The mother of the mother of X. In this case “\(mother(X)\)” is a subterm.

Literals are also called atomic formulas (or the negation thereof): that is, a predicate symbol applied to some terms. After the predicates are done with the terms, we’re on the level of logic: we just have a bunch of ‘trues’ and ‘falses’. The interesting part beyond the logical connectives (\(wedge\)s and \(\vee\)s) is the logical is the logical quantifiers: for all (\(\forall\)) and there exists (\(\exists\)). When working with CNF, one assumes that all variables are universally quantified. To be redundantly precise, one should write:

• \(\forall X (Human(X) \to Female(mother(X)))\)

Maybe we want to say that every human has a mother?

• \(\forall X (Human(X) \to \exists Y (Mother(X, Y) \wedge Y = mother(X)))\)

Which says that for every human, there exists a mother and that this mother equals the output of the mother function!

Wikipedia offers a good explanation of how to convert from standard first-order logic to conjunctive normal form. (The example is beautiful, too: “anyone who loves all animals is in turn loved by someone.” Pedantically, I’m not sure it’s true but 😋.) The basic idea is to remove implications and to move negations as far into the formula as possible. Then one renames variables to remove naming conflicts. Next, one moves quantifiers outward. Finally, one Skolemizes away the existential quantifiers. The trick is that if an entity exists, why not just pick a symbol to represent this? If the formula holds, we’ll still need to find an interpretation for the existential witness. These are called Skolem symbols and they functionally depend on all variables in an outer scope. As an example, let’s Skolemize the mother example:

• \(\forall X (\exists Y (\neg Human(X) \vee (Mother(X, Y) \wedge Y = mother(X) ) ) )\)
• \(\forall X (\neg Human(X) \vee (Mother(X, skolem_Y(X)) \wedge skolem_Y(X) = mother(X) ) )\)
• \(\neg Human(X) \vee (Mother(X, skolem_Y(X)) \wedge skolem_Y(X) = mother(X) )\)
• \((\neg Human(X) \vee Mother(X, skolem_Y(X))) \wedge (\neg Human(X) \vee skolem_Y(X) = mother(X) )\)

First, you can see that CNF is somewhat clunky and awkward in comparison. This is one motivation for theorem provers such as nanoCoP that aim to work with the logic in a “non-clausal” form that is closer to “how humans would write and think about the logic”.

Second, whoops, silly me! The Skolem symbol wasn’t really needed because I’d already been using a ‘mother’ function symbol! Thus only one more inference step is needed to fix my error, resulting in a fairly clean clause:

• \(\neg Human(X) \vee Mother(X, mother(X))\)

These are the ingredients that will go into the construction of the graph neural network (GNN).

HyperGraph Construction

The graph is constructed in such a way that there is a node for each clause, subterm, literal, function symbol, and predicate symbol.

The (hyper)edges then represent the structure of the formula. There are two multisets of edges:

• CT contains edges between clauses, \(C_i\), and the literals, \(T_j\), contained in them.
• ST contains edges among symbols, their terms, the arguments of the predicates or functions, and the polarity of the term (+/- 1).

Let’s do an example.

• Let’s call our clause, \(C_0 = \neg Human(X) \vee Mother(X, mother(X))\).
• The predicate symbols are, \(S_0 = Human\) and \(S_1 = Mother\).
• The function symbols are, \(S_2 = mother\)
• The literals are, \(T_1 = \neg Human(X)\) and \(T_2 = Mother(X, mother(X))\).
• The (sub)terms are, \(T_3 = X\) and \(T_4 = mother(X)\).
• And there’s a special term \(T_0\) to be used as a filler.

• Take the set of clauses to be, \(C = \{C_0\}\)
• The set of function and predicate symbols is, \(S = \{S_0, S_1, S_2\}\).
• The set of subterms and literals is, \(T = \{T_0, T_1, T_2, T_3, T_4\}\)

Now we can see that CT will contain edges: \(\{(C_0, T_1), (C_0, T_2)\}\).

The hyperedge set ST is more complicated:

• For \(T_4\): \((S_2, T_4, T_3, T_0, 1)\).
  • (In words: (mother’s node, this term node, X’s node, filler node, positive polarity))
• For \(T_1\): \((S_0, T_1, T_3, T_0, -1)\).
  • (Human’s node, this term’s node, X’s node, filler node, negative polarity)
• For \(T_2\): \((S_1, T_2, T_3, T_4, 1)\).
  • (Mother’s node, this term’s node, X’s node, mother(X)’s node, positive polarity)

If there are more than two arguments in a function or predicate, they are only encoded pairwise, i.e., for \(S_j(t_1,…,t_n)\) for \(n =geq 2\), the following edges are all added: \((S_j, T_i, t_k, t_{k+1},1)\). Below is an image of the hyperedges taken from Mirek’s presentation:

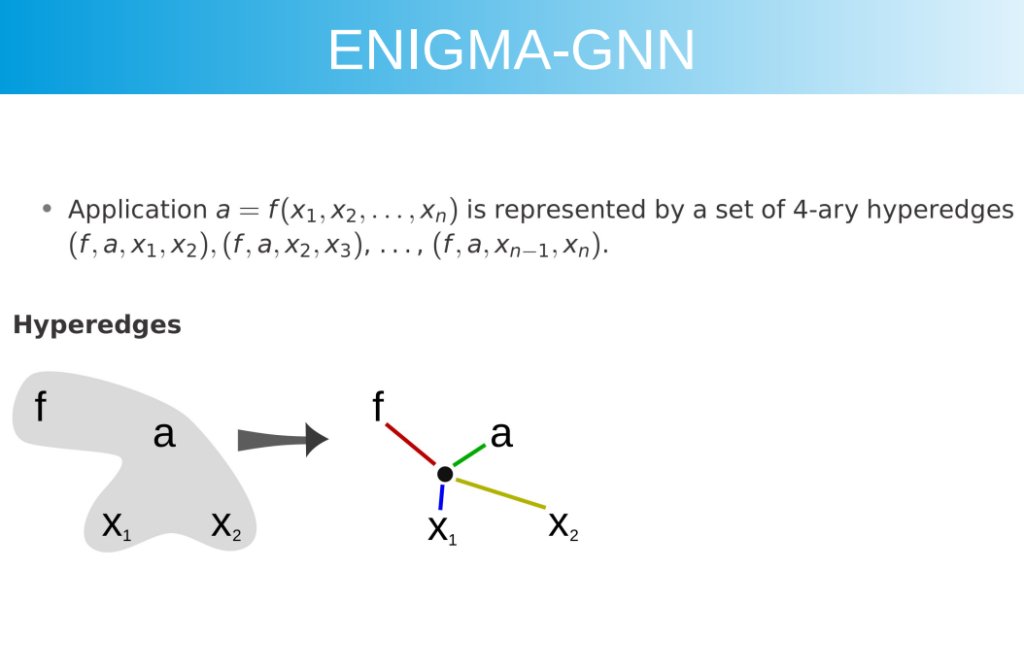
This encoding preserves argument order so that \(t_1 < t_2\) and \(t_2 < t_1\) will be encoded differently. But as noted in the paper, \(f(t_1,t_2,t_1)\) and \(f(t_2,t_1,t_2)\) will be encoded in the same manner.

A related quirk noted by colleague Jelle is that while the argument structure is technically represented, nuanced dependencies among arguments may be hard to figure out via the message passing based on these (hyper)edge sets. If one has a term t3, \(f(a,b,c)\), then node a and node c can only influence each other indirectly via node b or t3. What about the term t5 \(f(a,b,c,d,e\)? Nodes a and e can only interact in two hops via term node t5 itself. In this paper, 5 layers are used, so there seems to be a bottleneck. In our latest paper, The Isabelle ENIGMA, a 10-layer network is used for premise selection, which is a bit better.

I wonder if one could add more edges to help. The GNN is already resource-heavy and slow compared to the decision trees, however, so this experimentation could be non-trivial.

This is a pretty big improvement and a step in the right direction, in my opinion. 😊

Message Passing

The basic idea is to propagate information from a node to all its neighbors related by the edges (CT and ST). There are learned constant vectors to initialize clauses, symbols, and terms. Predicate symbols are initialized to zero.

One really cool feature of the network design is that the output should preserve the symmetry under negation where the embedding of node \(S_x\) should be the negative of the embedding of node \(\neg S_x\). I find this really inspiring: what structural, semantic features can be embedded directly into the neural network and its message-passing protocol?

In The Isabelle ENIGMA paper, we tried training separate initial type embeddings for all 2539 frequent types. This loses some of the anonymity. Ideally, one might add an extra node for each type so that “the GNN would learn to understand the types based only on their use in the current problem.”

The basic idea is that there are learnable bias vectors and learnable matrices as well as point-wise reduction operators (such as the max of every element in a collection of vectors concatenated with the average of every element in a collection of vectors).

• To update clause nodes, the literals in the clause are reduced and multiplied by a matrix. The clause’s embedding is also multiplied by a (different) matrix. These are both added together with a bias vector and passed through the ReLU function (which just sets negative values to zero).
• To update symbol nodes,
  • First, for each hyperedge with the symbol, the three terms are each multiplied by a separate matrix and added to a bias vector.
  • These values are multiplied by the polarity and reduced (by a different reduction operator).
  • This is then multiplied by yet another matrix, added to the symbol embedding multiplied by its matrix, and the hyperbolic tangent (because it’s an odd function that preserves negation).
• Updating term nodes is even more lengthy,
  • The term can appear in three positions in an ST hyperedge: as the term or as the 1st or 2nd argument in a pair. Thus for each of these possibilities, the two other terms and the symbol embeddings get multiplied by appropriate matrices and added to a bias.
  • These get reduced for each possible position of the term and again multiplied by a learnable matrix.
  • And as with the clauses, the embeddings of all clauses containing a term get reduced and multiplied by a matrix.
  • Then the term bias vector, the clause results, and the symbol-application results get added together with the term’s embedding multiplied by a matrix.
  • And then ReLU.

Conceptually, it seems like to update a node, the nodes connected to it are multiplied by a learnable matrix, reduced over (to mush them into one vector), and then multiplied by another learnable matrix (and added to a bias vector). The clause and literal messages are simpler.

What does it actually mean to multiply a matrix by a vector?

I’m glad you asked!

All linear transformations between two finite-dimensional vector spaces can be represented by a matrix multiplication and all matrix multiplications are linear transformations. Whereas functions such as ReLU and tanh (hyperbolic tangent) are non-linear. The dimensionality reduction operations are also non-linear.

Thus the “hypergraph neural network” is learning some linear transformations from a node’s neighbors and the node’s current embedding to output a new embedding. This is conceptually and visually rather simple. A few non-linearities are sprinkled on.

If you want to look at the actual equations, please just see the paper.

After some layers of this message passing (5-10 it seems), some standard neural network layers are applied to the output

---

Applications

This section will be rather brief, tho I’d love to dive into the details of each task with showy examples (and graphics beyond my capacity to easily construct). If anyone wishes to do so, please, be my guest ☺️😉

1. The GNN was used to guide leanCoP, a connection tableaux prover.
   • A Monte Carlo Tree Search is used, so the GNN provides estimated values of the proof search state as well as ‘action logits’, which get turned into the probabilistic distribution over actions via the softmax function.
   • The GNN proves 45.6% more on the test set and 49.5% more on the training set than rlCoP guided by XGBoost.
2. The GNN was tested on a DeepMath dataset of 32524 conjectures with 8 positive and 8 negative premises for each conjecture (all from the Mizar40 dataset). Achieving a classification performance of 80%.
3. The GNN can 65-60% of the time recover the symbol names from the mathematical structure on the DeepMath dataset. This is pretty cool.
   • About 40% of the data are newly introduced Skolem and definition symbols, so the testing accuracy is 78.4% if those are included.
   • Perfect naming of all symbols is only achieved for 544/3252 testing conjectures.
   • I wonder why this is less-than-perfect:
     1. There are common confusions such as “void and empty”, “associative and group-like, “in and c=”, and “closed and open”.
     2. Does the GNN just need bigger data or examples that specifically target these confusions?
     3. Does the GNN need to represent additional structural nuances a bit better?
   • These mistakes can lead to provable conjectures, however 😉
4. The GNN was used in ENIGMA Anonymous to guide the clause selection of E.
   • The final embedding of a clause and the aggregated embeddings of negated conjecture clauses are passed to a neural network to estimate the likelihood a clause will be ‘good’ or ‘not’.
   • The calls to the GNN are batched into queries (from size 64 to 512) because the evaluation is expensive.
   • Some processed clauses get added as context clauses to assist the GNN in its evaluation (from size 512 to 1536).
   • GNN training is very helpful.
   • The performance on Mizar was on par with the anonymous LightGBM (which is a first as the NNs are much slower).
   • The combined performance of both is 28,247 problems out of 57,880, which is about 4,000 better than the best performance by LightGBM. Complementarity is highly valued as once a problem is machine-proven, that data is easier to learn from.
   • The GNN seems to need fewer processed clauses to prove the same problems, which indicates that the guidance is becoming more intelligent.
5. The GNN is used in combination with a fast LightGBM model as well as with a Parental Guidance LightGBM model. See “Fast and Slow Enigmas and Parental Guidance” or the next post.
   • This included a GNN server to amortize the model loading costs.
   • The combinations of faster LightGBM models with the slower GNN model perform well
6. The GNN is used for premise selection on a large dataset of Isabelle problems. There are two rounds of premise selection with some theorem proving frenzies in-between. See The Isabelle Enigma for more details.
   1. Initially, on a 13,818 problem holdout set, E’s auto-schedule proved 6089 problems in 30 seconds.
   2. After two rounds of premise selection, E’s auto-schedule proved 7139.
   3. Vampire went from 6945 to 7397 problems solved.
   4. Pretty impressive that the GNN’s premise selection almost helped E to catch up to Vampire!
   5. Two-phase Enigma (with Parental Guidance and Clause Selection LightGBM models) performed better proving 7466 problems.
   6. CVC5 is perhaps the strongest automated theorem prover on this dataset and its performance went from 7140 to 7398.
   7. We barely managed to beat it 🥳

---

In summary, this (Hyper)Graph Neural Network is really cool.

I think there is still a lot of potential research development in this direction.

I’ve done work on trying to represent the state of a proof-search to the machine learners in various ways (such as via watchlist vectors or aggregating the feature vectors of the processed clauses).

In the GNN, one can just literally load in the contextual clauses.

Is this not a solid step toward the dream of neuro-symbolic integration in AI?