The Isabelle ENIGMA
I bet you can already guess that the topic of this research post and paper [official, slides] is to apply our ENIGMA work to the Isabelle proof assistant [w]. So far ENIGMA had been applied to the Mizar Mathematical Library, which is perhaps the largest library of formal math. The 3-phase ENIGMA proved 56% of the holdout set problems. And last year we announced that when combining many runs and time limits, a year ago, 75% of Mizar’s top-level problems have been automatically solved. We’d claim in papers that the core machine learning approach should transfer to other formal proof systems and some audience members would scratch their heads: “prove it.”
Long story short, we proved it.
I mainly ran the Parental Guidance and 2-phase ENIGMA training experiments in my usual chaotic good manner on the Isabelle.
Once the problems are in an appropriate TPTP format, such as FOF ((untyped) first-order form), E can clausify it into CNF (clause normal form) (See Geoff Sutcliffe‘s cute, concise recipe if curious how.) TPTP stands for Thousands of Problems for Theorem Provers and is both a language and a library of problems for theorem provers. Isabelle is typed, so we also try the TFF (typed first-order form), which required a small hack to the data preparation scripts to remove the types as the ENIGMA features don’t use them yet; moreover, we’re using anonymous features where predicate and function symbols are represented by their arity. The TFF worked quite far better than the FOF.
The GNN is only used for premise selection and Jan searched for E strategies and parameters that work well on the Isabelle dataset. The premise selection works really well, boosting E’s auto-schedule performance from 5,891/13,818 problems to 7,139 problems solved in the holdout set. CVC5 is apparently really strong; it’s an SMT (satisfiability modulo theories) solver. After 10 loops of training the 2-phase ENIGMA barely managed to defeat CVC5 and Vampire, however, all the provers are fairly close with the good premise selection 😏🤓:
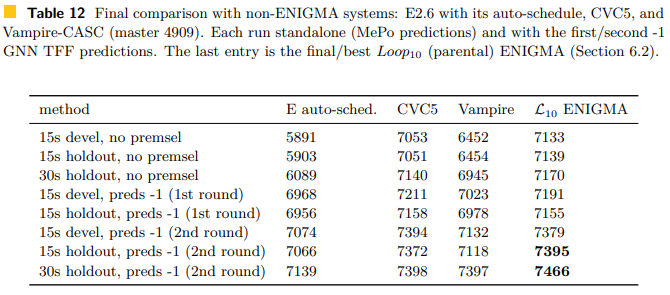
The best model proves 54% of the holdout set, so now that we know the LightGBM technology and GNN premise selection work well for Isabelle as well as for Mizar. Next up is the software engineering work to provide simple, convenient proof guidance as a service to Isabelle users, right? The AI transferred pretty well from Mizar, so sometimes the software engineering and data processing is the hard part.
On this topic, I find the Tactician‘s website really cool. The Tactician is a tool for Coq that learns from the tactic scripts you’ve already done and suggests tactics to advance a proof (or even tries to automatically complete the proof for you). At a glance, it appears Lasse et al have made the Tactician relatively easy to install and start using 🥳.
I’m not so well-versed in the particulars of Isabelle. I went through the exercises of a really good Coq for computational logic book and audited a course covering the basics of Lean, which is pretty similar to Coq. The process of translating one formal system into another in a manner that is easy to work with (and do theorem proving over) seems highly non-trivial. So the work described here is done by the co-authors 😊. I may use the royal ‘we’ for convenience 😉. I’ll describe a bit about the data including interesting tidbits I discovered while looking into the process. Please feel free to correct and educate me if I make naive errors below ;- ).
As an example, consider the MPTP2 (Mizar Problems for Theorem Proving) system implemented by Josef Urban to translate Mizar into sorted FOF, which is about 1300 lines of Prolog and 6000 lines of explanatory comments. Between versions 1 and 2, it seems the TPTP language was extended to encode types as predicates in the TPTP language because Mizar has syntactic weak types in that the types are represented like classifiers, e.g., “\(matrix(K, A)\), says whether \(A\) is a matrix of size \(K\) or not, and then this predicate can be used for type-dependent statements (such as that the multiplication of two \(K\)-sized matrices is also a matrix of size \(K\)). Definitions for abstract terms (defined by set comprehension, such as “all integers that are less than 0”). All my previous research work has been on data generated by the MPTP2 system. Might be there translations that help ENIGMA and ATPs (automated theorem provers) even more? Quite likely.
Fortunately, a lot of this work has already been done for us.
Isabelle has the Sledgehammer (🔨), a handy tool that clausifies subgoals one is working on and hands them to automated theorem provers. The Sledgehammer needs to choose some related, known facts from which the subgoal can be proved, too (‘premise selection’). If a clausal proof is found, it’ll be translated back into a list of Isabelle commands that can complete the proof. Thus the stronger the APTs, the more proof assistance one can get. Isabelle has three relevance filters for premise selection: the heuristic MePo filter (named after the authors: Meng–Paulson), MaSh, a machine learning based premise selector, and MeSh which combines MePo and MaSH. Given that we wish to use the GNN for premise selection, we use MePo to pre-select 512 relevant premises before translating the data to TPTP and the GNN premise selection is done on top of this.
Inspiration and Data
While we’d been thinking of applying ENIGMA to other ITP libraries than Mizar, the direct incentive now came from Sledgehammer developers asking for a suitable version of ENIGMA to test as they were testing “Seventeen Provers under the Hammer“: how well do the current provers perform on Isabelle and what input formats and translations work best? Apparently in 2010 such a survey was done in a “Judgment Day” paper, showing that E, SPASS, and Vampire could discharge half the typical goals users will run into — basically, the Sledgehammer is usable! 🔨🔨🔨
By the way, researchers in our group performed a similar survey of 19 provers and translations from HOL4 to TPTP in 2019: “GRUNGE: A Grand Unified ATP Challenge.”
Anyway, the Seventeen paper compares the performance for many parameters, such as how many premises to choose with the MePo filter: 512 and 256 are generally the best and similar. The ENIGMA version was trained on the TPTP library and didn’t perform well so we decided it’s high time to do a proper evaluation on our own.
Their survey indicates that the TF0 encoding works best. This is the native “monomorphic” encoding. I had to look this up. Isabelle has a limited implementation of “parametric polymorphism“, which means one can do things such as defining a generic type of lists, “List a”, for any type “a”. So this should work whether “a” is the type of “integers” or “strings”. I think the monomorphic encoding simply instantiates the variables to produce concrete types, e.g., “List Int” and “List String”. The authors expressed disappointment that the provers Leo-III and Zipperposition performed better in this setting despite having native support for polymorphism (which is possibly due to calling provers such as E in the back-end, which don’t support polymorphism). We also used this, which is a default for the Sledgehammer for E already.
For the FOF version, we used the “\(g??\)” encoding, which preserves the polymorphism in a complete manner and uses type guards. Type guards functionally encode types by acting as predicates, e.g.: if X is of type “List Int”, then bla bla bla. Looking at Seventeen, it turns out that the monomorphic version, “\(\tilde{g}??\)”, generally performs better and most systems support TF0, which performs even better, anyway.
Another really basic term I didn’t know is “lambda lifting” (λ-lifting). I think this resembles the process of clause normalization outlined in the GNN post. The idea is to take local, nested functions with free variables and to give them explicit parameters in such a manner that they can be ‘lifted’ to the global scope. This way the functions are easier to reason about (for the ATPs, not necessarily for the human programmers).
Wikipedia uses the following example of a program that adds numbers from 1 to \(n\):
def sum(n):
def add(x):
return n + x
if n == 1:
return 1
return add(sum(n-1))Note how the nested function “add(x)” uses the variable “n” implicitly based on the context. This can be lifted out as follows:
def lifted_add(n,x):
return n + x
def sum2(n):
if n == 1:
return 1
return lifted_add(n, sum2(n-1))Now the adding function is separate, so the code should look easier to play with (however this is an anti-feature if one wishes to avoid polluting the global scope with many named functions). This example is a bit silly because now it’s clear that there was no need to define a special function: this is just “plus”!
def sum3(n):
if n == 1:
return 1
return n + sum3(n-1)This is even simpler, right? The Quicksort example on Wikipedia seems more realistic: the “swap” and “partition” functions are very particular to this sorting algorithm. A bigger reason why this example is silly is that Gauss discovered a very neat trick for summing the numbers from 1 to \(n\)! In the case of \(n = 100\), it looks like this:
The solution can be simply algebraically calculated: 100 * (100+1) / 2. In general:
def sum_gauss(n):
return n * (n+1) // 2I was curious if using the math is actually more efficient in Python. The lifted version is 2.4 times faster than the original; the version that uses “+” normally is 3.4 times faster than the original; and gauss’s summation trick is 31.8 times faster. For what it’s worth, using a for-loop instead of recursion is 13.8 times faster so the math is still best. Even simple formulas save a lot of time over simple code. Hail math!
It’s called lambda lifting because λs are used to represent generic functions (a la lambda calculus). For example, “λx.x” is the identity function that maps each x to itself, and “λx.λy.(\(x^2\)+\(y^2\))” would be a sum-of-squares function. These should all be given names, which can seem a bit clunky. Another fun example of the use of nested functions I saw is for functions that return functions:
def get_power_function(k):
def power(x):
return x**k
return power
cuber = get_power_function(3)
#cuber(3) -> 27Functions being input and output of other functions is pretty cool, right?
I’d like to learn a bit more about this 🕳🐇, such as in what manner these encodings can be incomplete. One of us has, I believe, proposed the terminology “theorem-increasing” and “theorem-decreasing” to specify the way in which two encodings can be misaligned.
Anyway, lambda-lifting is used for both the non-polymorphic TFF and the polymorphic-encoded FOF we use in the experiments.
In the Seventeen paper, which is easy enough to read, they tried various combinations of λ-lifting and SKBCI combinators to deal with Isabelle’s λ-abstractions. A really inspiring result is that the higher-order E performed best on TH0 (many-sorted, not polymorphic, higher-order logic). This might mean that we can train ENIGMA on the higher-order versions and won’t need to rely on these tricks for encoding higher-order functionalities as much? 🤩
We use the Mirabelle tool of Isabelle to export the goals/problems encountered when building Isabelle “sessions” (a collection of theory files, a bit like a project in an IDE). Each entry from the Archive of Formal Proofs (AFP) constitutes a session. Seventeen takes 5000 problems from 50 sessions from the AFP. Our dataset is created by exporting 179 sessions (and 1902 theory files) from the AFP, Isabelle 2021-1, and the IsaFoR library (Isabelle Formalization of Rewriting).
I looked at a survey on “Mining the Archive of Formal Proofs” and it seems that the Archive of Formal Proofs in Isabelle contains 215 articles and 146 of these are indexed under computer science, which means some of the problems should be somewhat different from the mathematical Mizar ones. However, it seems that most of the largest sessions are mathy:
Some theory files come with Isabelle’s installation. I found it really easy to download, set up, and to poke around some math formalizations. 🤓. Actually following the math would take more energy, however, 😋. Below is the ‘example’ in the directory for HOL/Nonstandard_Analysis:
Quite tellingly, the Mirabelle export resulted in 293,587 FOF problems and 386,619 TFF problems, which we aligned to get the 276,363 problem dataset (with 248k for training and 13.8k for small training, development, and holdout sets). Names are rather inconsistent compared to Mizar’s TPTP data, so the symbol-name anonymizing ENIGMA is even more important.
Comparing 88,888 problems from the FOF dataset with 113k problems from the Mizar dataset, minimizing the premises needed for an ATP proof, it seems that on average, the Mizar problems have 3.5x as many clauses and 4-5x as many variables — moreover, iProver can nail almost all of the Isabelle ones in 10s whereas in Mizar it gets closer to half of them. (The ‘i’ in iProver stands for ‘instantiation’.) Perhaps the Isabelle data being more ground and non-equational makes sense given various sub-goals users would see are included?
Hypotheses are also used more in the Isabelle dataset. The datasets are pretty different.
That’s about it for the data. There’s a lot I still don’t know about the particulars of logical representations of mathematics and computer science.
One point that surprises me is how important the particular details of the encoding are. It’s not like one can just sketch out a basic language to express (many-sorted) first-order logic and be done with it.
As discussed in an earlier post, while a unary representation of numbers is easy to theorize about it’s practically pathetic. There are fun arguments that senary (base-6) could be better than the usual decimal (base-10) for actual (human) usage. It turns out US basketball uniform numbers are restricted so that referees can signal players via senary hand signals!
From a general AI point of view, this means that flexible use of representation languages becomes necessary. The AGI will be held back if it needs to depend on careful human curation of data and reasoning languages: it needs to be able to craft and reason about domain-specific languages on its own! This brings us to the topic of the MeTTA system that Ben Goertzel, Jonathan Warrell, Alexey Potapov, and Adam Vandervorst are working on: “a meta-probabilistic-programming language for bisimulation of probabilistic and non-well-founded type systems.” If one works in a generic language for rewrite systems over (meta)graphs, then one can simulate other type systems and reason about those as well as writing ‘normal’ code. This seems to lead down the category-theoretic homotopy type theory 🕳🐇 with guarded cubical type theory. Wolfram’s “Ruliad” model for trying to abstractly study physics a la “all possible rewrite systems” also ends up in this direction:
And in the end the ruliad actually seems to be the ∞-category of ∞-groupoids, or what’s called the (∞,1)-category.
I’d love to grok this theory more 🤤. Skimming half a dozen pages on ncatlab.org has helped a lot with gaining rudimentary intuition for categories but the infinitary category theory is still more beyond me than I’d like. At present, I’d venture that category theory appears to be the future of mathematics. The concept of internal logic has helped me to make sense of logical foundations; it’s the idea that categories with sufficient structure can internally represent certain logics. Topos theory appears to be a generalization of Set theory (where Set is a topos): “nice places to do math1.” There seem to be open questions as to how to concisely and effectively work with the theory in practice, yet once those kinks are worked out, people will probably shift over without much hesitation 😋.
This ties in with an interesting result of both our and Seventeen’s results: TFF trumps FOF. And the latest version of E supports some higher-order logic, so THF beat TFF. An interesting caveat is that technically many-sorted higher-order logic is model-theoretically ‘equivalent‘ to many-sorted first-order logic. Perhaps soon enough groundwork will have been done that untyped FOF will fall out of favor and we’ll shift toward using typed and higher-order expressions as they can finally out-perform FOF?! Theoretically, the higher-order formats are clearly ‘better’ but they’re harder to work with due to their expressivity.
Tuning
Jan and Josef had previously invented 550 strategies on Mizar, Sledgehammer, and some other datasets. So the first step is to run these to see if a good strategy to use with ENIGMA can be found. Little f1711 was found, which when adding SInE (basically premise selection) performs a bit better than E’s auto-mode. After doing some training with ENIGMA, SInE actually ceases to be needed, especially after the GNN’s premise selection. 😏
When clausifying formulas, theorem provers have to choose when to introduce definitions for sub-formulas. E’s heuristic is to count the occurrences of the sub-formulas and to add definitions beyond some threshold, which was experimentally optimized to be 24 long long ago in a galaxy far far away. I find the comparison with human languages interesting: after how many times of describing a concept, will you wish to coin a new word? I think sometimes we can go far over 24! What if we were more trigger-happy with the neologisms? I think that’d be interesting 😏.
Anyway, E’s clausification to FOF was timing out on 10% of the problems. We did some experiments. The definitional-cnf threshold of 3 is the largest for which there were no timeouts in 60 seconds. We also did performance checks with and without SInE: 3 was 1st and 2nd. The threshold value of 3 seems to result in the largest file sizes, too! Some of the initial data with the value of 24 made it into the results before we switched to 3, but let’s roll with it 😏.
ENIGMA
Once the data issues are set aside, the ENIGMA training proceeds as usual. Because the ENIGMA features separate conjecture clauses, we decided to treat hypothesis clauses in the same manner (which may not be ideal but seems better than nothing).
Jan did the ENIGMA clause selection model experiments and I did the parental guidance experiments; Jan’s tests were more systematic in that did both FOF and TFF experiments starting from scratch. With the deadline nigh, there’s a lot of fiddly experimentation to do to see if the technology can work, so it’s hard to do things neatly — at least that’s my excuse 😛. So
On the FOF data, the SInE baseline scored 3,5k/13.8k on the development set and by the third loop, the no-SInE ENIGMA scored 3.9k Whereas on the TFF data, the no-SInE baseline scored 5.5k and the no-SInE ENIGMA scored 5.9k by the third loop. Setting the learning aside, it’s already fairly clear that the TFF is the appropriate format to work with.
This data is used to train the GNN model for premise selection. Two rounds of premise selection are done, with some ENIGMA training and data generation loops in-between. I find it interesting how we can get away with stripping the TFF formulas of the type information in the first round. Given E is stronger on the TFF, the learning doesn’t have to be perfect.
The GNN scores the premises and we use two ways to choose the best:
- Take the top-k premises as a slice, for k in \((16, 32, 64, 128, 256)\).
- Take all premises with a score above k in \((1,0,-1,-2,-3,-4)\).
Needless to say, the \(-1\) sliced worked best, which is probably because the GNN can mess up a bit and missing a crucial premise is a fatal error.
For the second round, to adapt the GNN to the many-sorted data, separate initial embeddings are trained (apparently as part of the neural network via backprop) for all 2539 types that occur more than 10,000 times. This is no longer anonymous, so future work will probably involve adding anonymous type-nodes that only reflect their use. The \(-1\) slice still performs best on a 200 problem development set. We also chose a complementary slice in each round to diversify the training.
Anyway, the baseline strategy, f1711 without SInE, proves 6.7k/13k on the development set now, which is a bigger increase than we attained by training clause selection models. After maybe 4-5 loops of training, Jan trimmed the data to include at most 6 proofs per problem and proved 66994 problems. Timewise, we didn’t make it to doing a thorough test of the second premise selection model with the clause selection only ENIGMA.
In parallel to the above, I was having fun with the Parental Guidance model. I like to say that “diversity is strength.” My approach here was to develop as strong performance as possible in time, even at the cost of introducing some chaos.
I first started with the FOF data, too, which wasn’t going that well. When switching over to the TFF data, I decided to mix the FOF and TFF data out of curiosity (especially because some problems were solved in the FOF version but not in the TFF version). I’m not sure this helped with raw performance but it may have added some diversity to the proofs or greedy cover of problems solved. 🤷♂️🤪
The general modus operandi was to find a greedy cover of ENIGMA runs that cover the total problems solved and to use all the data from the runs in the greedy cover, not minding the duplicate proofs. I chose what models (and parental guidance threshold parameters) to run on the full training data based on the greedy cover over a 300 problem development set. In hindsight, I think Jan’s infinite-looping strategy of data curation is probably better: just keep a proof-base of 3-6 proofs per problem.
I also tried using both the clause selection models trained on my data as well as the best models Jan developed in combination with the parental guidance model. Usually, Jan’s model was better. I think this might in part be due to his model’s data being part of the training data as well as due to being a static strategy that the learning can adapt to. This suggests a different training protocol where I first train a clause selection model, run ENIGMA with this to gain new data, and then train a new Parental Guidance model. Maybe alternating which model I train? Seems worth a try 🤓.
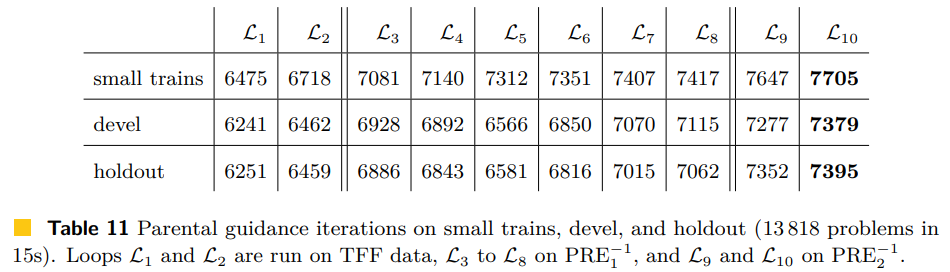
Looking at the results below of 10ish loops of training on the TFF data, I find it cool how the biggest jumps come from the premise selection (but overall the learning adds more). We’ve shown that the 2-phase ENIGMA works on the Isabelle data and that the GNN premise selection helps a lot (even for other ATPs that Sledgehammer works with).


One Reply to “The Isabelle ENIGMA”
Comments are closed.